D3 三角剖分模块
本文主要介绍 d3-delaunay 模块
德劳内三角剖分 Delaunay Triangulation 是一个计算机几何的概念,该算法可以将一系列 (x, y) 二维点连起来,构成一个三角网格,并且让这些数据点不落入任何一个三角形的外接圆中,以尽量避免出现 “sliver” triangles 「极瘦」的三角形(夹角过小)。
而维诺图 Voronoi diagram 是德劳内三角剖分图的 dual graph 对偶图,该图也是基于一系列 (x, y) 二维点绘制而成的(但是并不是将数据点相连,而是对它们进行分隔,实际是将德劳内三角剖分所得三角网络中的一系列三角形的外接圆的圆心相连),将这些数据点所在面积划分,所得的每一个小区域只包含一个数据点,并且这个数据点是位于这个小面积的「中心」(即该区域中任意点,到该「中心」数据点的距离,都比到其他数据点都要短)
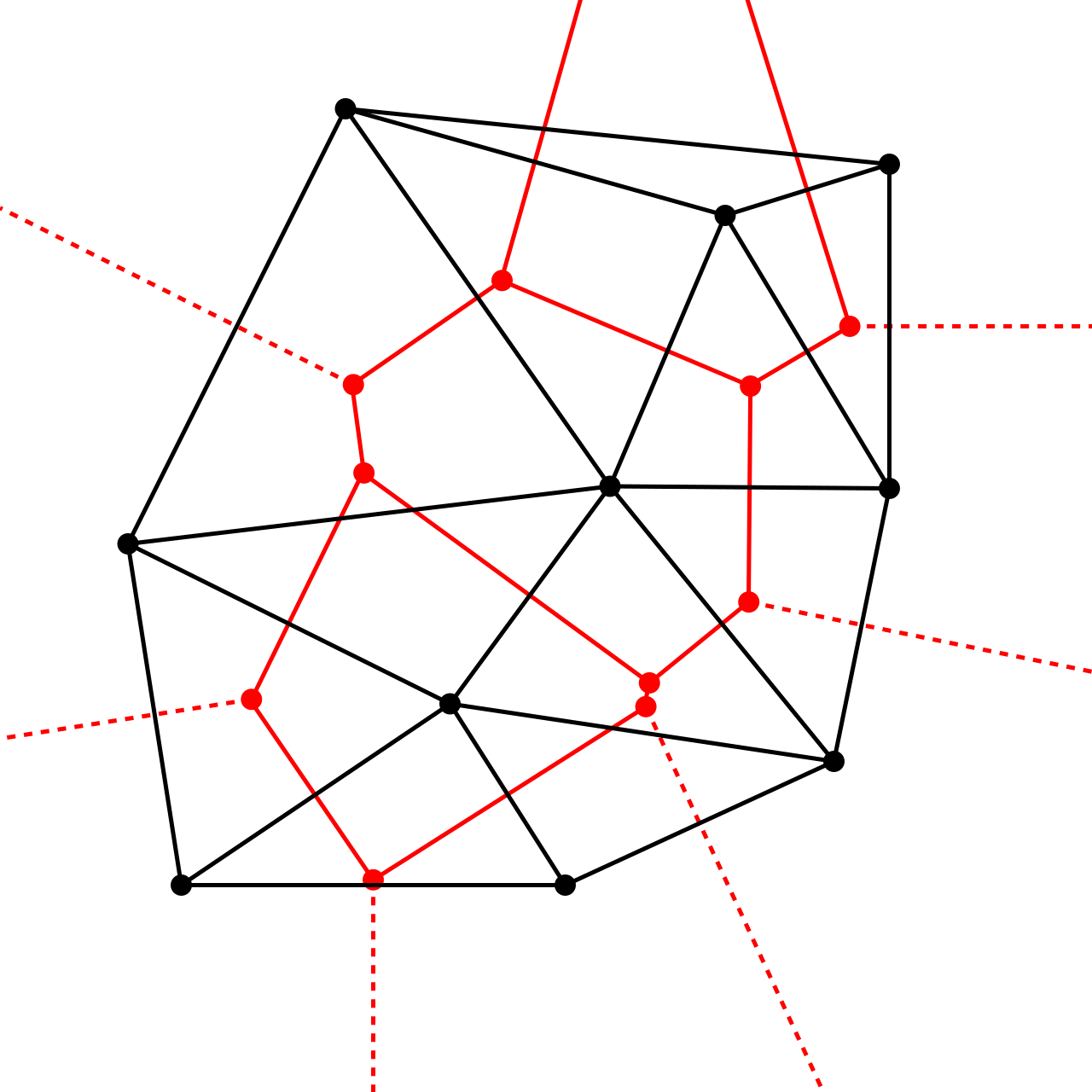
d3-delaunay 模块提供了一些方法用于绘制 Delaunay Triangulation 德劳内三角剖分图和 Voronoi diagram 维诺图
提示
该模块使用了 sweep 扫描算法来计算三角剖分,具体采用的是一个名为 delaunator 的 JS 库
Delaunay Triangulation 三角剖分

使用 new Delaunay(points) 或 d3.Delaunay.from(points, fx, fy, that) 方法对给定的数据点(集)计算三角剖分,返回一个对象(在以下文段简称为 delaunay 三角剖分器)
但是两者所接收的参数和数据集形式有所不同
new Delaunay(points)传入的数据集points是一个扁平化的数组,而二维平面上的每一个点的都需要两个数值表示(x, y),所以points数组的元素是[x0, y0, x1, y1, ...]依次用每两个一组来表示数据点的d3.Delaunay.from(points, fx?, fy?, that?)传入的数据集points(所支持的默认形式)是一个嵌套数组[[x0, y0], [x1, y1], ...]每一个元素都是一个二元数组以表示二维平面上的一个点。
如果传入的数据集不是前面所述的形式,则需要同时给出横坐标值和纵坐标值的 access handler 访问函数fx和fy,D3 会对数据集中的每个元素分别调用这两个方法,以获取该数据点所对应的横纵坐标值
第四个(可选)参数that用于更改在 access handler 访问函数fx和fy中的this的指向, 💡 这和 JS 原生方法 Array.from 类似
提示
使用方法 d3.Delaunay.from() 计算三角剖分的速度一般比 new Delaunay(points) 更慢,由于它需要进行额外的步骤获取每个数据点所对应的横纵坐标值
所以在该模块的内部,存储数据点的坐标值时采用的是扁平化数组的形式,以便提高效率
以上方法返回一个三角剖分器 delaunay,它是一个对象,具有一些属性和方法
说明
三角剖分器 delaunay 的属性和方法的返回值一般都是数组,但是里面元素的值并不是数据点,而是用于指向数据点的索引值
另外需要区分数据点的索引值,并不是直接对应到原始数据集的,因为传入的数据集是扁平化数组,即 positionData = [x0, y0, x1, y1, ...] 的形式,这个数组依次每两个元素才表示一个二维平面的点(横纵坐标值)
所以要根据数据点的索引值来获取到数据点的横纵坐标值,就需要进一步转换,假如要获取第 i 个数据点的坐标值,则它对应到原始数据集的两个元素的索引是 2i 和 2i+1,数据点的索引值 i 与原始数据集(扁平化数组)的索引值存在两倍关系,则该数据点的横纵坐标值是 [positionData[2i], positionData[2i+1]]
以下是三角剖分器 delaunay 的一些属性:
- 属性
delaunay.points返回该三角剖分器所基于的数据集,一个扁平化的数组[x0, y0, x1, y1, ...] - 属性
delaunay.triangles返回一个数组,包含所有计算得到的三角形的顶点
由于三角形有三个顶点,所以该数组的元素的排序是有规律的,依次每三个一组[i0, j0, k0, i1, j1, k1, …]以表示一个三角形的三个顶点(这些点在三角形上沿逆时针顺序排列),例如i0, j0, k0表示第一个三角形的三个顶点(索引值),i1, j1, k1表示第二个三角形的三个顶点(索引值)注意
该数组中这些元素的值并不是顶点的坐标,而是所对应的数据点的索引值(⚠️ 注意不是原始数据集的索引值,两者关系看前面 ☝ 的说明)
因为三角形网络 triangular mesh 是通过将数据点连接起来所构成的,所以三角形的顶点也就是数据点,这里通过索引值进行对应
但是由于三角形存在共边(共用顶点)的情况,所以这里返回的数组的元素值(数据点的索引值)也会有重复
例如在 Canvas 中画出第
i个三角形jsconst { points, triangles } = delaunay; const t0 = triangles[i * 3 + 0]; const t1 = triangles[i * 3 + 1]; const t2 = triangles[i * 3 + 2]; // 基于数据点的索引值从原始数据集(扁平化的数组 points)获取其横纵坐标值时,索引值的映射是 2 倍关系 context.moveTo(points[t0 * 2], points[t0 * 2 + 1]); context.lineTo(points[t1 * 2], points[t1 * 2 + 1]); context.lineTo(points[t2 * 2], points[t2 * 2 + 1]); context.closePath(); - 属性
delaunay.hull返回一个数组,表示凸包凸包
凸包 convex hull 是指包含了所有数据点的最小凸多边形
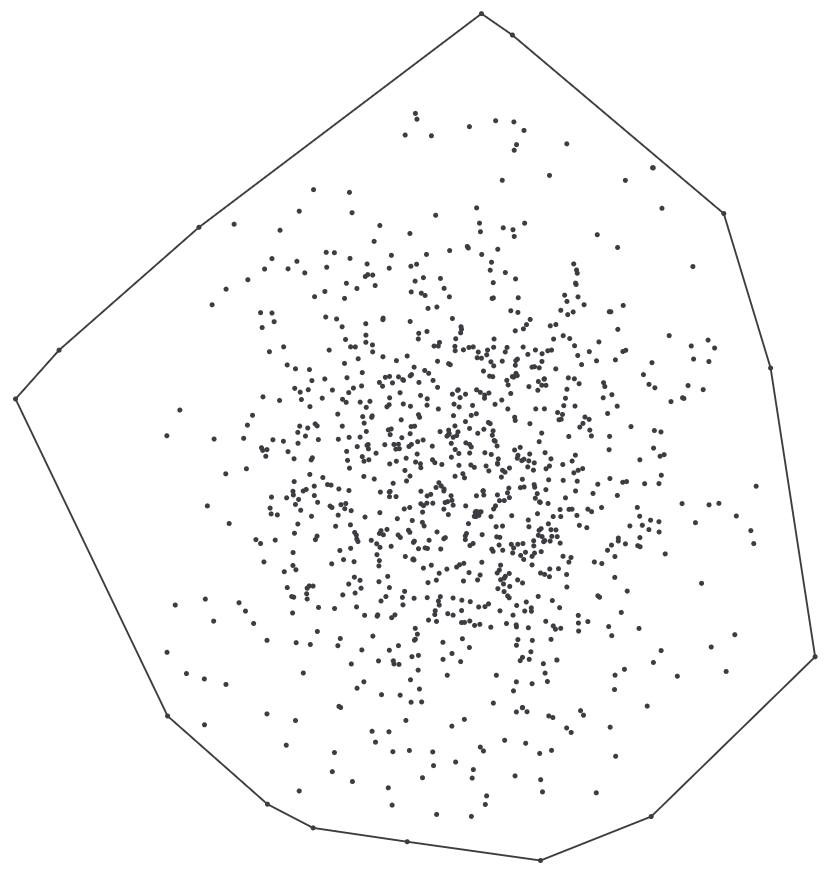
凸包 可以直观地将其理解为将位于最外周的一系列数据点连起来所构成的路径
该数组中这些元素的值并不是坐标值,而是数据点的索引值(这些点在凸包上沿逆时针顺序排列)提示
如果要需要得到数据点的具体坐标值,需要将索引值经过转换再映射到原数据集(扁平化的数组)中
positionData = [x0, y0, x1, y1, ...]读取出来基于数据点的索引值从原始数据集(扁平化的数组 points)获取其横纵坐标值时,索引值的映射是 2 倍关系
例如该数组的第一个元素的值为
v1(它表示第v1个数据点位于凸包上),对应到原始数据集可以得到这个点的横纵坐标值是[positionData[2*v1], positionData[2*v1+1]] - 属性
delaunay.halfedges返回一个数组,包含所有半边半边的定义
该模块使用一个名为 Delaunator 的 JS 库计算三角剖分,其中涉及到一个概念是「半边」
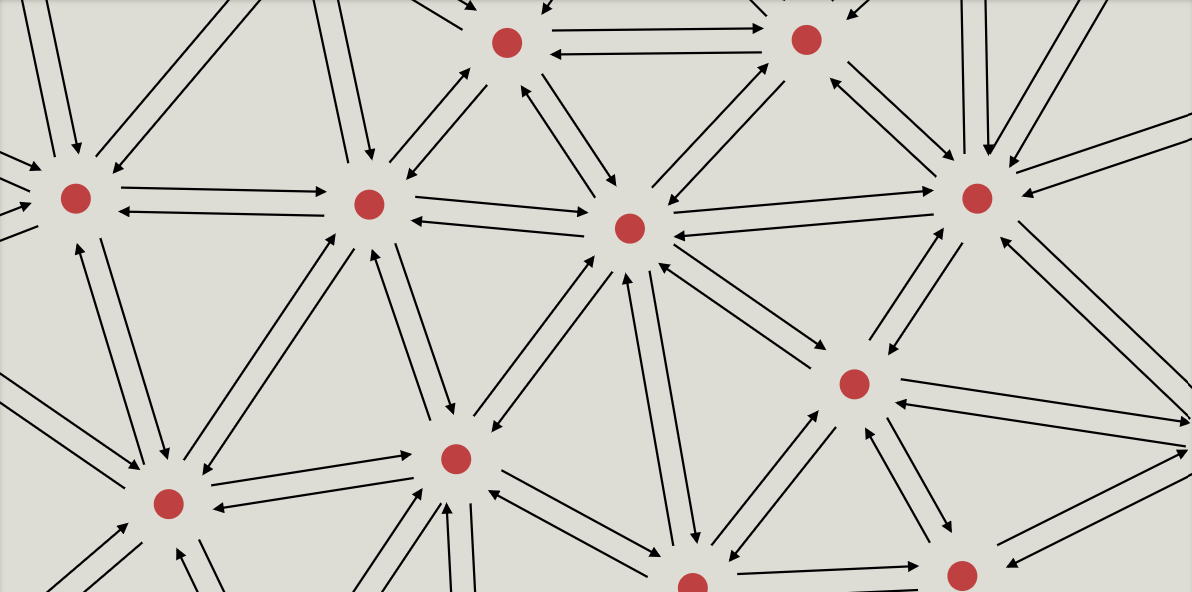
半边 由于在三角形网络中,相邻的三角形存在共用的边,在该算法中将共用的边,看成是由两条重叠的、方向相反的「半边」构成,这样就可以实现将每条边都划归对应到唯一的一个三角形 ❓ 将双向的共用的边,变成了具有唯一方向的半边,便于遍历和索引
所以半边的概念只是在该算法中特有的,而且是仅针对相邻三角形共用的边,对于位于网络的外周的边,它们没有被两个三角形共用,所以它们并没有相应的半边
该数组中这些元素的值只是一个数值,但是它可以表达一条边。但从数学的角度而言,一般两个点才可以决定一条边,所以在使用这个数组时,还需要结合元素的索引值i
该数组中元素的索引值i,同时也是充当三角形顶点数组的索引值(即前面所提到的属性delaunay.triangles所返回的数组);而该元素的值j=delaunay.halfedges[i]也是作为索引值,可以用来对应到三角形顶点数组的元素。通过这两个索引值i和j,就可以从三角形顶点数组中获得两个元素(顶点/数据点),以表示一条半边提示
三角形顶点数组的元素排序是有规律的,依次每三个一组,以表示一个三角形的三个顶点
所以该数组的索引值也是三个一组,例如
0, 1, 2、3, 4, 5等,可以对应到三角形顶点数组的元素,也是表示一个三角形的三个顶点如果在该数组中,划分到同一个三角形
I的 3 个元素,它们的值依次为 ,通过这些值可以在三角形顶点数组中找到对应的元素,它们归属于不同的三角形,这些三角形都是于三角形I相邻的这就以下这段话(出自官方文档)的意思
Equivalently, this means that triangle ⌊i / 3⌋ is adjacent to triangle ⌊j / 3⌋. If j is negative
其中
⌊和⌋符号(注意不是[]中括号)表示向下取整在数组中会看到有些元素的值为
j=-1不能作为索引值在三角形顶点数组中找到对应的元素,这是由于在网络的外周的边没有被两个三角形共用,所以某些三角形的顶点是不能构成半边的
可以使用该属性绘制出所有位于三角剖分网络内部的边(不包含凸包上的边)jsconst { points, halfedges, triangles } = delaunay; for (let i = 0, n = halfedges.length; i < n; ++i) { const j = halfedges[i]; // 由于半边是将真实的一条边(相关相连三角形的共边)「分裂」为两条,在绘制时只需要挑其中一条即可 // 这里通过 j < i 条件判断来跳过两条半边的其中一条,而且 i 是从 0 开始的(非负数),也可以筛掉 j=-1 的情况 if (j < i) continue; const ti = triangles[i]; const tj = triangles[j]; context.moveTo(points[ti * 2], points[ti * 2 + 1]); context.lineTo(points[tj * 2], points[tj * 2 + 1]); } - 属性
delaunay.inedges返回一个数组,表示入射半边入射半边
入射半边 incoming halfedge 也是和前面 ☝ 所说的「半边」概念类似,也具有方向性
它们是用于遍历三角形网络,从一个数据点开始,沿着从它发出的入射半边(路径)可到达下一个数据点,以此类推,可以遍历整个三角剖分
虽然每个点都有多条边与之相连,但是为了遍历的一致性,对于每个点只选择一条半边作为入射半边,规定如下:
- 对于重合的数据点,只为其中一个点设置入射半边(重合的数据点位于二维平面的同一个位置,不需要重复遍历)
- 凸包上的点,入射半边采用位于凸包上的边
- 其他的点,任意选择一条半边(但是保证了半边只有一个顶点想对应,以保证可以遍历整个三角网络,而不会出现重叠的路径 ❓ )
入射半边的定义也是 Delaunator 算法特有的 ❓ 且针对特定的一次遍历操作而言,不同的操作选择生成的入射半边可能不同
该数组中这些元素的值只是一个数值,和前面 ☝ 所说的「半边」一样,在使用这个数组时,还需要结合元素的索引值i,才可以知道是哪两个顶点构成的边
该数组中元素的索引值i,同时也是充当三角形顶点数组的索引值(即前面所提到的属性delaunay.triangles所返回的数组);而该元素的值e=delaunay.inedges[i]也是作为索引值,可以用来对应到三角形顶点数组的元素。通过这两个索引值i和e,就可以从三角形顶点数组中获得两个元素(顶点/数据点),以表示一条入射半边
在数组中会看到有些元素的值为e=-1表示它是重复的数据点,不能作为索引值在三角形顶点数组中找到对应的元素,这是因为重复的数据点位于二维平面的同一个位置,不需要重复遍历
以下是三角剖分器 delaunay 的一些方法:
delaunay.find(x, y, i)根据传入的二维平面的位置(x, y)返回一个最相近的数据点的索引值
第三个(可选)参数i用于指定从哪一个数据点(该参数是表示数据点的索引值)开始遍历三角形网络的数据点,默认值为0提示
如果要需要得到数据点的具体坐标值,需要将索引值经过转换再映射到原数据集(扁平化的数组)中
positionData = [x0, y0, x1, y1, ...]读取出来基于数据点的索引值从原始数据集(扁平化的数组 points)获取其横纵坐标值时,索引值的映射是 2 倍关系
例如该返回的值为
index(它表示第index个数据点),对应到原始数据集可以得到这个点的横纵坐标值是[positionData[2*index], positionData[2*index+1]]delaunay.neighbors(i)根据传入的数据点(索引值)i,返回与之相邻近的一系列数据点(一个数组,包含这些数据点的索引值)说明
如果数据集中存在重复的数据点,则当方法
delaunay.neighbors(i)传入的索引值指向的是一个重复的数据点,则返回值是undefined,因为最靠近的点是与之重叠的重复数据点 ❓ 但是没有实际的用途delaunay.renderPoints(context, radius)绘制所有数据点(一个个小圆形)
(可选)参数context是画布 Canvas 的绘图上下文,作为绘制区域提示
如果有设置
context参数,则这些小圆形会被渲染到指定的画布上下文中,否则返回一个路径字符串(用作 svg 元素<path>的属性d的属性值)
(可选)参数radius用于设置(数据点)小圆形的半径大小,默认值为2delaunay.hullPolygon()返回一个表示凸包的嵌套数组[[x0, y0], [x1, y1], …, [x0, y0]],它的每个元素是一个二元数组[xi, yi]表示凸包上的一个数据点(横纵坐标值)凸包
凸包 convex hull 是指包含了所有数据点的最小凸多边形
可以直观地将其理解为将位于最外周的一系列数据点连起来所构成的路径
delaunay.renderHull(context)绘制出凸包凸包
凸包 convex hull 是指包含了所有数据点的最小凸多边形
可以直观地将其理解为将位于最外周的一系列数据点连起来所构成的路径
(可选)参数context是画布 Canvas 的绘图上下文,作为绘制区域提示
如果有设置
context参数,则这个多边形会被渲染到指定的画布上下文中,否则返回一个路径字符串(用作 svg 元素<path>的属性d的属性值)delaunay.trianglePolygon(i)返回一个嵌套数组,表示第i个三角形。
该数组中有 4 个元素[[x0, y0], [x1, y1], [x2, y2], [x0, y0]]每个元素都是一个二元数组,表示三角形的一个顶点的横纵坐标值。提示
虽然三角形是由三个顶点构成的,如果使用 Canvas 画布来绘制,可以通过调用方法
closePath自动闭合路径,则只需要三个顶点的坐标值即可而为了兼容 SVG,则需要给出第 4 个元素(与第一个元素相同),让路径回到第一个顶点,形成闭合的三角形
delaunay.trianglePolygons()返回一个迭代器,可用于 JS 的循环结构中,依次读取到一个三角形(以数组[[x0, y0], [x1, y1], [x2, y2], [x0, y0]]的形式表示),从而遍历得到所有的三角形提示
其实该迭代器内部是调用
delaunay.trianglePolygon(i)方法,所以每次迭代所返回的值,都是一个表示三角形顶点坐标值的数组delaunay.renderTriangle(i, context)绘制出第i个三角形
(可选)参数context是画布 Canvas 的绘图上下文,作为绘制区域提示
如果有设置
context参数,则三角形会被渲染到指定的画布上下文中,否则返回一个路径字符串(用作 svg 元素<path>的属性d的属性值)delaunay.render(context)绘制出三角剖分网络的所有边
(可选)参数context是画布 Canvas 的绘图上下文,作为绘制区域提示
如果有设置
context参数,则三角形网格会被渲染到指定的画布上下文中,否则返回一个路径字符串(用作 svg 元素<path>的属性d的属性值)delaunay.update()重新计算三角剖分。当三角剖分器所依赖的数据集发生变化时,可以调用该方法进行更新
Voronoi diagram 维诺图
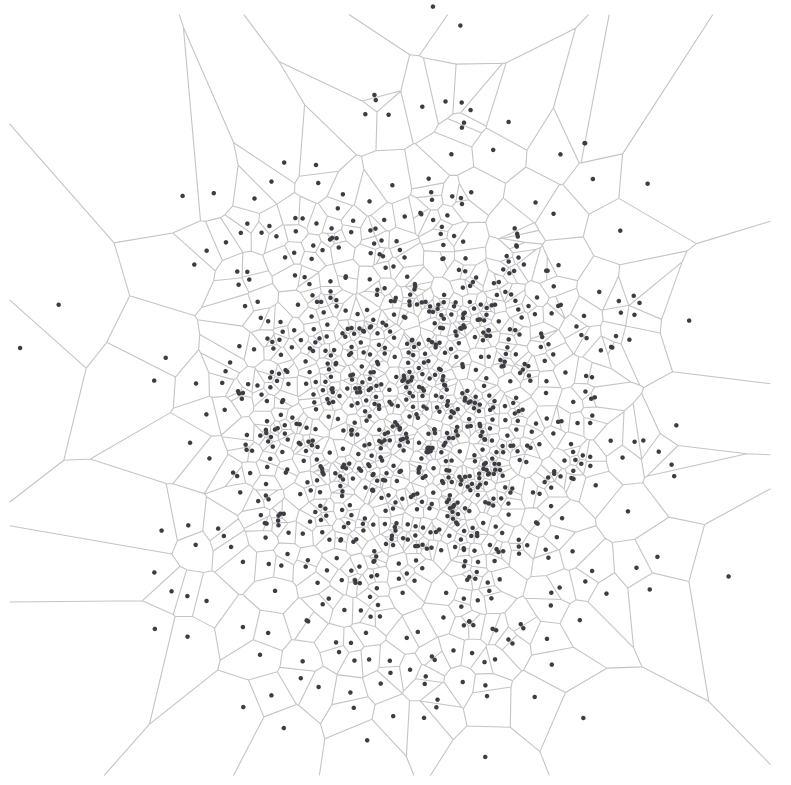
使用方法 delaunay.voronoi(bounds) 生成一个维诺图生成器(在以下文段简称为 voronoi)
其中参数 bounds 表示维诺图面积的边界,用一个四元数组 [xmin, ymin, xmax, ymax] 来表示平面上的两个点(可以指定一个矩形区域),以约束所生成的维诺图的面积,默认值是 [0, 0, 960, 500]
提示
参数 bounds 控制视图的大小,该值只会影响某些与绘制维诺图相关的方法 voronoi.render()、voronoi.renderBounds()、voronoi.renderCell()(它们的具体介绍看 👇 下面文段)
说明
根据维诺图的定义,它会根据数据点 points 对给定的面积区域 bounds 进行划分,得到的一系列的小区域,称为 cell 单元格
其中每个单元格包含一个数据点,所以单元格的索引值和数据点的所以值一一对应
维诺图生成器是使用 delaunay 三角剖分器的方法生成的,所以需要先基于数据集生成一个 delaunay,再调用delaunay.voronoi(bounds) 生成所对应的维诺图生成器
维诺图其实是基于三角剖分图生成的,大概流程如下:
- 基于数据集(一系列的二维平面的点)进行三角剖分,得到三角形网格图
- 计算每个三角形的外接圆的圆心
- 将相邻三角形所对应的外接圆圆心连起来,得到维诺图的内部面积(大部分)划分
- 再处理边缘面积的划分
可以参考 The Delaunay’s Dual 这个 Notebook,它对该算法/步骤给出了交互式的演示介绍
提示
当数据集中只有 1 或 2 个数据点,甚至数据集为空的场景,是无法通过三角剖分生成三角形网格,但是对于这些特殊的情况,该模块有提供回退兜底方案,也可以返回维诺图生成器,对面积进行合理划分
维诺图生成器 voronoi 是一个对象,具有一些属性和方法
以下是维诺图生成器 voronoi 的一些属性:
- 属性
voronoi.delaunay返回该维诺图生成器所关联的三角剖分器 delaunay voronoi.circumcenters返回一个数组,表示所有(通过三角剖分所得的三角形的)外接圆的圆心
这是一个扁平化的数组[cx0, cy0, cx1, cy1, ...]依次每两个元素一组,cx, cy表示一个圆心的横纵坐标值- 属性
voronoi.vectors返回一个数组,表示一系列的构成开放单元格的半边开放单元格
Open/infinite cell 「开放单元格」是指位于维诺图最外一周的那些非封闭的单元格,这种单元格只有在靠近中心的一侧被边所包围,向外延伸的部分没有边包围而是被视图所裁切。每个开放单元格都会有两条边延伸到视图边缘,就像是射线一样,所以将它们称为 vectors
这些射线不是通过连接外接圆的圆心而成的,而是基于相邻的这些有限长度的边(这些有限长度的边就是通过连接外接圆的圆心而成的)计算而成的,以便对边缘的区域进行合理的划分
返回的是一个扁平化的数组,所以元素依次是每两个一组(表示一个点的横纵坐标值),而一条线需要两个点确定,所以实际应用时是将四个元素看作一组(对应 vector 两个端点的横纵坐标值 ❓ )[vx0, vy0, wx0, wy0, ...]可以绘制出射线的路径
在数组中会看到大量元素的值为0因为大部分的边都是通过连接外接圆的圆心而形成的有限长度的边,它们并不是维诺图的外周 vectors,所以在该数组中它们所对应点的坐标值都设置为0 - 属性
voronoi.xmin、属性voronoi.ymin、属性voronoi.xmax、属性voronoi.ymax分别返回一个数值,表示维诺图的视图边界[xmin, ymin, xmax, ymax]
以下是维诺图生成器 voronoi 的一些方法:
voronoi.contains(i, x, y)返回一个布尔值,以表示第i个 cell 单元格是否包含二维平面的位置(x, y)提示
也就是原始数据集的第
i个数据点(与其他数据点相比)是否距离(x, y)位置最近该方法并不受视图 bounds 的约束,即传入的位置
(x, y)可以是视图范围之外的,也可以判断给定索引值i所对应的单元格是否「包含」位置(x, y)voronoi.neighbors(i)返回一个数组,表示与第i格 cell 单元格相邻的单元格(以它们的索引值表示)提示
由于维诺图的 cell 单元格与数据点一一对应(每个单元格包含一个数据点),所以维诺图的单元格相邻关系,与数据点的相邻关系是一致的
但是由于维诺图的大小会被视口 bounds 约束,所以该方法所返回数组的元素,应该是相应的三角剖分器的方法
delaunay.neighbors(i)所返回数组的元素的子集voronoi.renderBounds(context)绘制出维诺图的视口边界
(可选)参数context是画布 Canvas 的绘图上下文,作为绘制区域提示
如果有设置
context参数,则三角形网格会被渲染到指定的画布上下文中,否则返回一个路径字符串(用作 svg 元素<path>的属性d的属性值)提示
该方法的作用等价于以下代码
jscontext.rect(voronoi.xmin, voronoi.ymin, voronoi.xmax - voronoi.xmin, voronoi.ymax - voronoi.ymin)voronoi.cellPolygon(i)返回一个嵌套数组,表示第i个(闭合的)cell 单元格。
该数组的形式是[[x0, y0], [x1, y1], ..., [x0, y0]]每个元素都是一个二元数组,表示单元格(凸多边形)一个顶点的横纵坐标值。提示
如果使用 Canvas 画布来绘制,可以通过调用方法
closePath自动闭合路径,则只需要数组只需要依次列出所有顶点的坐标值即可而为了兼容 SVG,则需要在最后一个元素重复第一个元素,让路径回到第一个顶点,形成闭合的凸多边形
voronoi.cellPolygons()返回一个迭代器,可用于 JS 的循环结构中,依次读取到一个单元格(以数组[[x0, y0], [x1, y1], [x2, y2], [x0, y0]]的形式表示),从而遍历得到维诺图的所有单元格提示
其实该迭代器内部是调用
voronoi.cellPolygon(i)方法,所以每次迭代所返回的值,都是一个表示单元格(凸多边形)顶点坐标值的数组voronoi.renderCell(i, context)绘制出第i格 cell 单元格
(可选)参数context是画布 Canvas 的绘图上下文,作为绘制区域提示
如果有设置
context参数,则三角形网格会被渲染到指定的画布上下文中,否则返回一个路径字符串(用作 svg 元素<path>的属性d的属性值)voronoi.render(context)绘制出维诺图(所有边)
(可选)参数context是画布 Canvas 的绘图上下文,作为绘制区域提示
如果有设置
context参数,则三角形网格会被渲染到指定的画布上下文中,否则返回一个路径字符串(用作 svg 元素<path>的属性d的属性值)voronoi.update()更新维诺图生成器。
一般在数据集发生变化时,调用该方法进行更新,该方法也会同时更新维诺图生成器对应的 delaunay 三角剖分器