线性插值法
参考
线性插值的原理是假设两个点 和 之间呈线性关系(即通过直线来连接两个点)
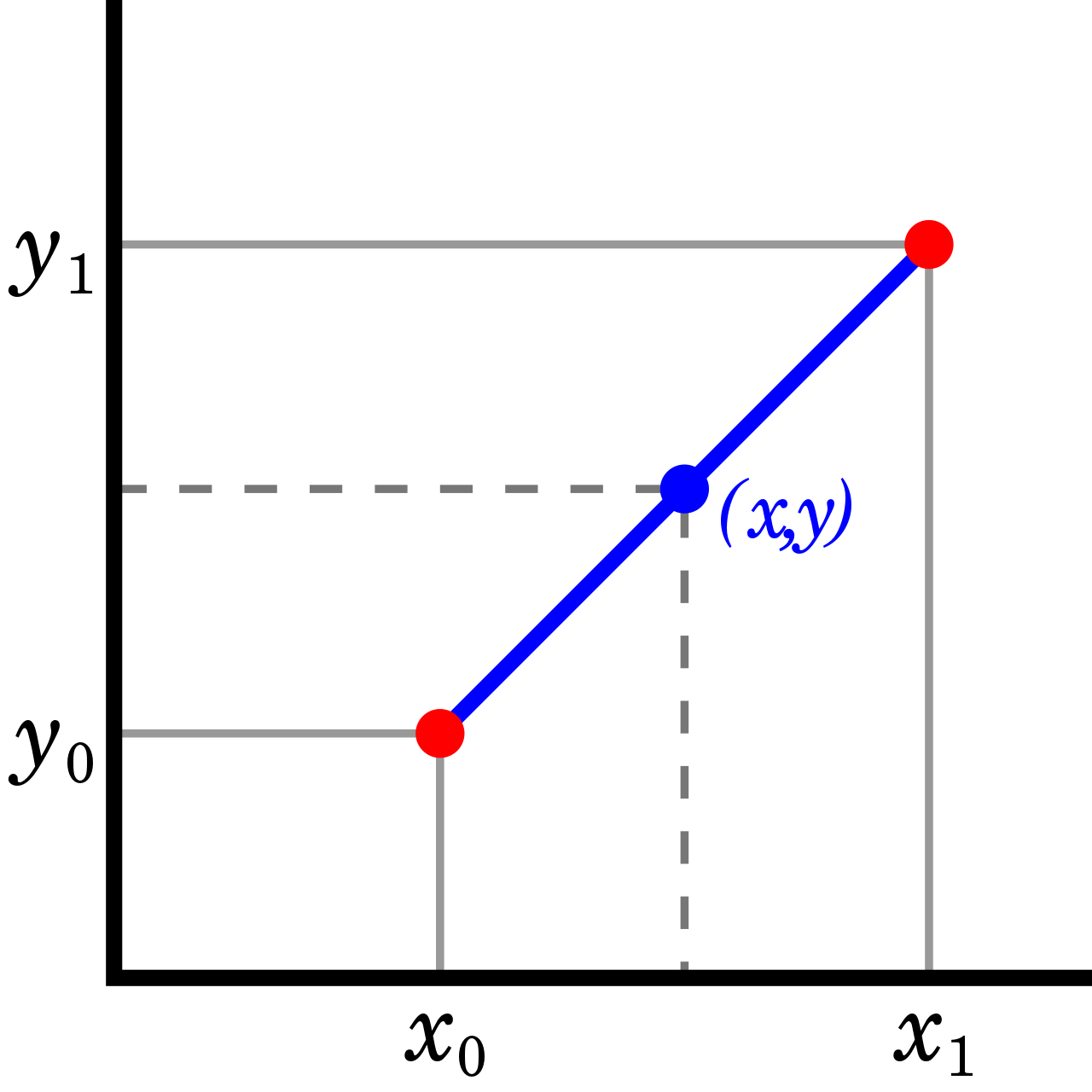 线性插值
线性插值
说明
通过两个端点估算给定的横坐标 所对应的纵坐标值
那么就可以根据比例关系(直线处处的斜率相同)计算出其中某个点的值
化简得到
从公式可以看出 的值由 分别与 和 的差值所决定
由于 是 差值的系数,而 是 差值的系数,所以当所求的点 靠近 时,则 差值接近于 ,因此最终结果中 的比重就少;反过来当所求的点 靠近 时,则 差值接近于 ,因此最终结果中 的比重就少
或者将公式进行变换,可以更容易看出这个关系
与 相乘的部分包含 ,而与 相乘的部分则是包含对应的 ,这样分析观察更有一致性
由于 的差值项前面的系数都是 负数,所以两个端点对 的「影响」大小,跟所求点 与相应端点的距离远近是呈负相关的关系
说明
其中 和 被称为权重,以衡量相应的点(它们相应的系数)对于最终的 值的影响,也称为归一化距离 normalized distances,因为它们的和是
还可以用符号来替代分式公式,得到以归一化距离 normalized distances来表示的公式,更简洁一些
用 来表示在横轴水平上,所求点 与左侧端点 的距离占总距离的比例
所以 值公式可以表示为
提示
如果假设在外延部分也是满足一样的线性关系,也可以估算出在 范围之外的值
