D3 层级结构数据模块
参考
本文主要介绍 d3-hierarchy 模块
许多数据集从从本质上是嵌套结构的,如行政地理等级数据,文件存储系统数据等,一个好的层次数据可视化作品,能促进多维度的推理分析,既可以对单个单元进行微观的观察,也可以从整体进行宏观的观察。
提示
即使原始数据不属于层级结构数据,也可以通过一些经验和方法转换为层级结构数据,并进行合适的可视化,例如 k-means 聚类,以及系统发育树。
d3-hierarchy 模块提供了几种经典的技术实现对层次结构数据的可视化:
- 节点-连线图 Node-link diagrams:用图形元素表示节点和连接(节点之间的关系),以展示拓扑结构。例如用圆点表示一个节点,并用线段连接父子节点。
此类可视化技术的一些常见的图像:- tidy tree 紧凑的树状图:其排版特点是让各层级的节点对齐,并充分利用空间,让图形所占的面积最小化
- dendrogram 树状图:其排版特点是让所有的叶子节点(在树图的最后)对齐,这样会让图形看起更「舒展」、更清晰
- Indented tree 缩进树状图:其排版特点是让节点的浏览和(缩展)交互更方便(类似于目录树结构)
- 毗邻关系图 Adjacency diagrams:使用节点的相对位置展示拓扑结构,这种展示方式将每个节点编码为定量的区域。例如使用区域大小表示收入或文件大小。
此类可视化技术的一些常见的图像:- icicle diagram 冰柱图 使用矩形来表示定量区域
- sunburst 旭日图 使用环形的一小段来表示定量区域
- 包裹图 Enclosure diagrams:也是一种区域编码,但是通过相互包裹的形式来展示拓扑结构。
此类可视化技术的一些常见的图像:- treemap 树图 以递归的方式将一个区域细分为一个个小矩形,而且根据层级关系会存在相互包裹的矩形。
- circle-packing diagram 圆堆图 以圆形的方式来细分区域,虽然并不比 treemap 利用空间区域的效率高,但是更易于通过拓扑结构显示数据的层级结构
计算层级结构
在使用 d3.tree() 等方法进行可视化布局之前,需要先使用 d3.hierarchy(data) 对数据进行层级结构计算,为节点添加相应的属性。
d3.hierarchy(data[, children])根据指定的树形数据data构建层级结构(计算每个节点的层级信息)。最后返回根节点对象(里面也包含所有的子孙节点对象),节点对象在以下称为node注意
指定的数据
data必须为一个表示根节点的对象(里面包含子孙节点数据)。例如以下的 JSON 数据json{ "name": "root", "children": [ {"name": "child #1"}, { "name": "child #2", "children": [ {"name": "grandchild #1"}, {"name": "grandchild #2"}, {"name": "grandchild #3"} ] } ] }
第一个参数data是层次结构数据。
第二个(可选)参数children是子节点数据的访问函数 accessor function,(从根节点开始)每一个节点都会依次调用该函数。该函数需要返回一个可迭代对象(一般是数组),作为该节点的children属性值,表示该节点所包含的子节点集合。其默认值(访问函数)如下js// 假设在层次结构数据 data 中,每一个节点所包含的子节点集合都是在 children 属性中 function children(d) { return d.children; }说明
d3-array 模块有相关的方法
d3.group()和d3.rollup()对扁平的数据(如数组)进行分组归类,并返回一个 Map 类型的数据。这些方法最后返回的是一个 InternMap(这是 D3 基于 Map 类型进行增强的自定义数据类型,它和对象类似,也是以 key-value 键值对的形式存储数据),属于可迭代对象。
因为通过分组归类后返回的 Map 也是具有层级结构的,所以
d3.hierarchy(data)也是支持传入一个 Map 作为数据data,采用不同的方法来解析里面的层级关系,最后也是返回出一个根节点对象。虽然不管入参的是一个树形对象还是一个 Map,最后返回的都是一个根节点对象
root整体结构一致,但是有一个细节应该注意,就是每个节点所绑定的数据node.data。因为 Map 中每一项都是通过 key-value 来表示的,键和值都是重要且具有意义的(这和树形对象不同,因为它的每一项的属性都是固定的,也就是说属性名并没有包含特定的信息),所以在计算层级结构时,会将每一个 Map 转换为一个每一个节点所绑定的值都是一个二维数组
[key, value]并作为该节点所绑定的数据,其中key对应于该分组的分类依据,value对应于该分组中所包含的成员。如果
d3.group或d3.rollup采用了多个分组依据,那么一些中间的节点所绑定的数据就是[key, InternMap],其中key对应于该分组的分类依据,而InternMap就是该分组所包含的子分组如果是叶子节点则绑定具体的值,即在原始的数组(未进行分组归类的扁平结构)中的相应元素
另外传入的 Map 就是根节点的数据,而根节点并不属于任何分组,所以 D3 会自动将其转换为一个二维数组
[undefined, Map]作为根节点所绑定的数据如果传入
d3.hierarchy(data)的数据是一个 Map,D3 会针对 Map 的结构特点,默认采用另一种子节点数据的访问函数 accessor functionjs// 如果传入的数据是一个 Map,则采用以下的子节点数据的访问函数 function children(d) { // 如果当前节点所绑定的数据形式是 [key, value] 一个数组 // 则提取第二个元素 value 作为该节点所包含的子节点 // 否则表示该节点是一个叶子节点,它没有子节点 return Array.isArray(d) ? d[1] : null; }例如对于以下的数据,先通过
d3.group()进行分组归类,再使用d3.hierarchy()计算层级结构jsconst data = [ { name: "jim", amount: "34.0", date: "11/12/2015" }, { name: "carl", amount: "120.11", date: "11/12/2015" }, { name: "stacy", amount: "12.01", date: "01/04/2016" }, { name: "stacy", amount: "34.05", date: "01/04/2016" } ] // 先基于名称 name 进行分组 // 再基于日期 date 进行分组 const group = d3.group(data, d => d.name, d => d.date) // 计算层级结构 d3.hierarchy(group)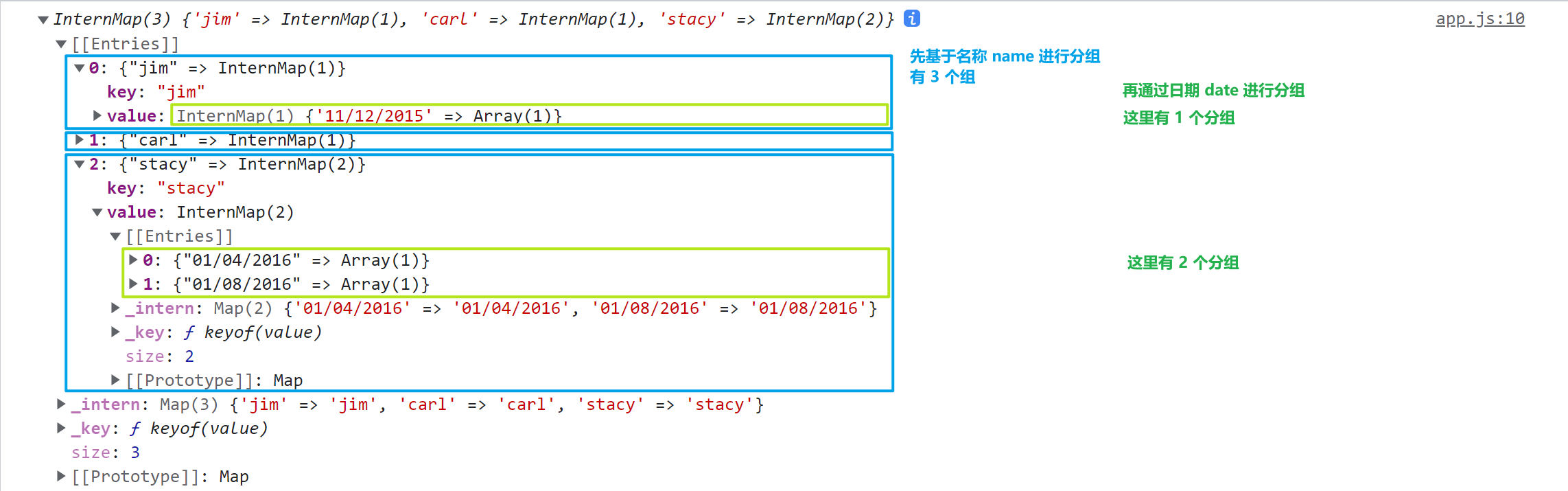
d3-group 分组归类 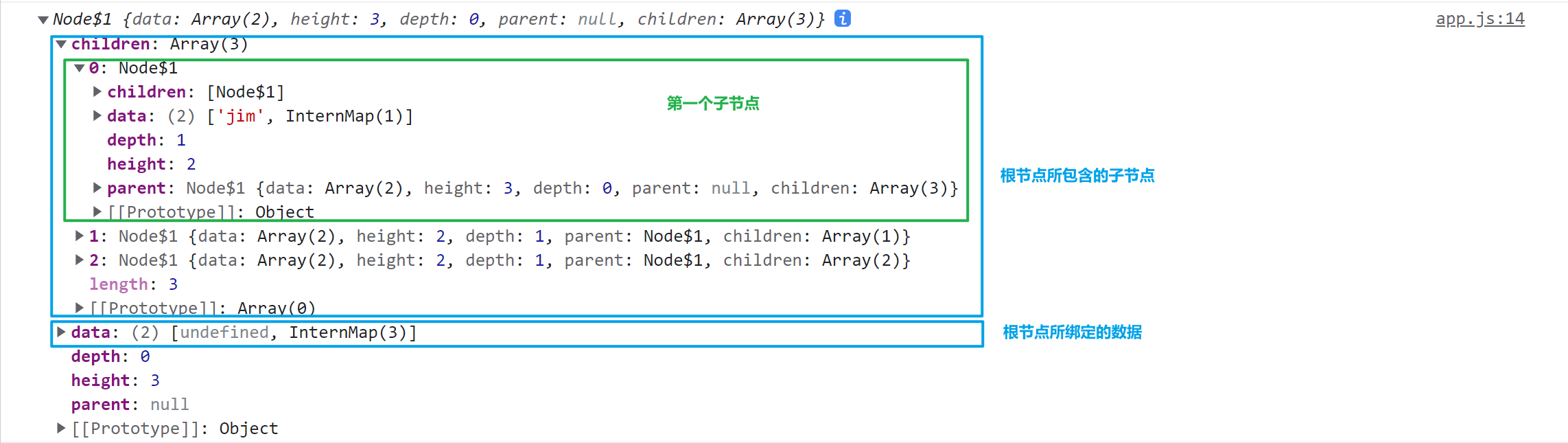
d3-hierarchy 计算层级结构 关于 d3-hierarchy 如何处理 Map(可迭代对象)数据可以参考这个 issue 的讨论
对于前面提到的 JSON 示例数据,通过d3.hierarchy(data)获得一个根节点对象(里面也包含所有的子孙节点数据)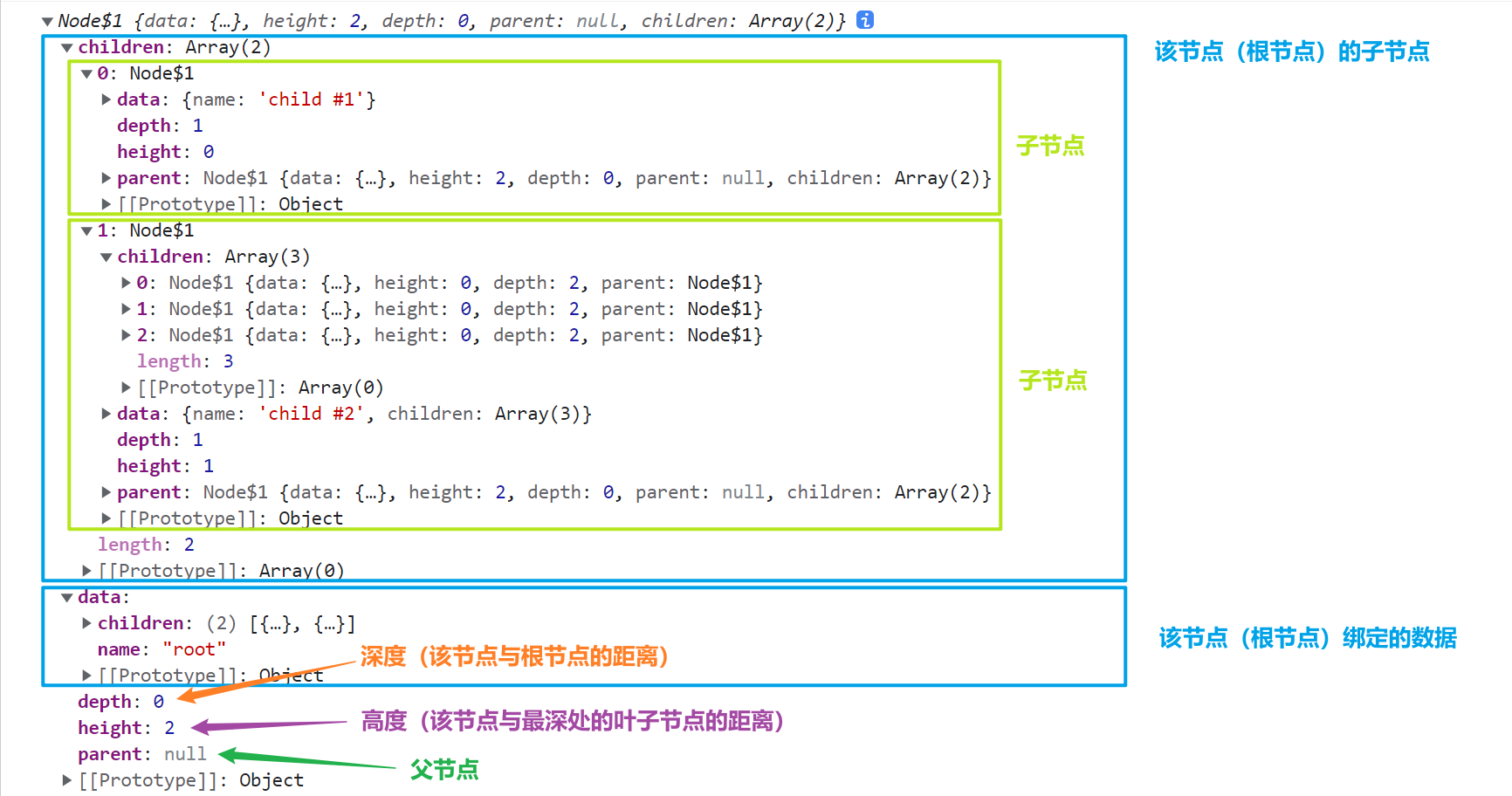
d3-hierarchy 结果
返回值的每一个节点对象都会附加以下属性:node.data当前节点所绑定的数据,由 D3 在计算层级结构时分配指定node.depth当前节点的深度,即该节点与根节点的距离,根节点为0,每增加一个层级(后代)就增加1node.height当前节点的高度,即该节点与其分支后最远的叶子节点之间的距离,叶节点为0node.parent当前节点的父节点,根节点的父节点为nullnode.children一个包含节点的数组,表示当前节点所包含的直接子节点(如果有的话),叶节点的子节点为undefinednode.value(可选属性)当前节点以及后代节点 descendants 的总计值,通过调用节点的方法node.sum()或node.count()计算后才添加到节点上
节点是一个可迭代对象(因此可以通过调用一个特殊的方法 node[Symbol.iterator]() 生成一个「迭代器」),更一般的用法是直接在循环结构中使用,如 for-of 结构:
// 依次遍历该节点(包括当前节点)所在的分支后的所有节点
// 从当前节点 `node` 开始遍历
// 直至分支后最远端的叶子节点
for (const descendant of node) {
console.log(descendant);
}
节点对象具有一些实用的方法:
node.copy()复制该节点对象(包含该分支后的子孙节点)。
这样在复制所得的节点对象中,虽然子孙节点的信息依然保留完整,但是会丢失了原来的父节点信息,即当前节点node变成根节点,即node.depth=0,而其父节点是node.parent=null注意
虽然复制节点对象时,会包含其后的子孙节点,就像是「深拷贝」。
但是该操作实际上并不是完全是深拷贝,因为复制得到的节点和原来的目标节点所绑定的数据(对象)是共享的(这样做是为了节省性能?因为节点所绑定的数据可能比较大?)
node.ancestors()返回一个数组,由当前节点以及它的祖先节点构成(包括自身节点,作为数组的第一个元素,然后按照层级结构,依次列出上一级的节点,所以最后一级的节点是根节点)node.descendants()返回一个数组,由当前节点及它的所有后代节点构成(包括自身节点,作为元素的第一个元素,然后按照层级结构,依次列出同层级的节点,即先列出子层级的所有节点,再列出孙子层级的所有节点,并依次类推,列出所有后代节点)node.leaves()返回一个数组,按照遍历顺序列出该节点所在的分支后的所有叶子节点(叶子节点就是那些没有子节点,即没有children属性的 node 节点对象)node.find(filter)从当前节点(包含)所在的分支后的节点里寻找满足filter条件的节点,并返回第一个满足条件的节点,如果没有找到满足条件的节点就返回undefined。
参数filter是一个筛选函数。从当前节点(包含)开始,该分支后的节点会依次调用该函数,并以节点自身作为参数传入filter(node)该函数最后返回一个布尔值,以表示节点是否符合条件node.path(target)获取当前节点node到目标节点target的最短距离的路径,以一个数组表示,其中各元素是路径经过的节点。
比较复杂的场景是当前节点node和目标节点target并是互为祖先/子孙节点的关系,而是在不同的分支上,则数组中节点的顺序是从当前节点开始 ⤴️ 先向上一级回溯的父节点 ⤴️ 依次类推 ⤴️ 直至寻找到当前节点与目标节点的最近的共有祖先节点;然后再朝着目标节点向下一级移动 ⤵️ 向下一级节点 ⤵️ 依次类推 ⤵️ 直达目标节点。(前面所述的复杂过程是在两个节点并不在同一个分支上的普遍情况,如果两个节点正好在同一个分支中,则不需要向上回溯或向下移动的其中之一,即路径是单向的,所以数组中节点的关系也会更简单,只是父/子的单向关系)说明
通过以上方法可以寻找在层级结构数据中的节点之间的最短路径,而最短路径对于使用 依层级进行连线捆绑 Hierarchical Edge Bundling 技术进行节点关系可视化时十分有用。
node.links()返回一个数组,里面的元素表示当前节点及其后代节点之间的所有连线(即从当前节点开始,该分支上所有节点之间所构成的所有连线)。
每根连线以一个对象表示,该对象有两个属性source和target。其中属性source其值是连线一端的节点(父节点),另一个属性target则是连线另一端的节点(子节点)node.sum(value)求出该分支上各节点(计算到当前节点为止)的累计和,并为各节点添加一个属性node.value表示到相应节点时的累计值。该方法最后返回的还是该节点对象,便于链式调用。
入参value是一个求值函数,按照后序遍历的顺序(即从叶子节点开始),该分支上的节点依次调用该求值函数,并传递节点所绑定的数据作为参数value(d)。该求值函数需要返回一个数值,以表示当前节点的值。注意
该方法的一个重要副作用是为分支上的所有节点(从叶子节点到当前节点为止)添加上
node.value属性。另外需要注意
node.value并不是单纯地由上面提及的求值函数value的返回值构成,而是还要加上其直接子节点的值正如该方法
node.sum(value)的名称所言,它最后为各节点所添加的属性node.value是累计值疑问
在官方文档中提到求值函数要返回一个非负数的数值
The function is passed the node’s data, and must return a non-negative number.
这可能是因为该方法求的是累计值,如果有的节点的求值函数返回的是正数,有的返回负值,则最后各节点添加的属性
node.value的值看起来就不像是累加值?(那为什么所有节点都返回负值就不可以呢 :satisfied: 绝对值看起来也是不断增大呀)提示
默认情况下,为分支上各节点添加的属性
node.value是累计值,既包括当前节点的值,也包含分支上(直到叶子节点)其他节点的值。但如果想
node.value属性只表示当前节点所在分支的叶子节点的累计和(只反映分支末尾的叶子节点的情况,而不必考虑途径的中间节点),可以在求值函数value(d)中对节点是否含义子节点进行判断,如果该节点有子节点(即中间节点)就让求值函数最后返回0;只有当该节点没有子节点时(即叶子节点)才让求值函数返回相应的正数值。这也是一个常见需求,计算节点所在的分支上最后所拥有的叶子节点数量
js// 这里只有叶子节点所绑定的数据上,才具有 d.value 属性 const flare = { "name": "flare", "children": [ { "name": "analytics", "children": [ { "name": "cluster", "children": [ { "name": "AgglomerativeCluster", "area": 3938 }, { "name": "CommunityStructure", "area": 3812 }, { "name": "HierarchicalCluster", "area": 6714 }, { "name": "MergeEdge", "area": 743 } ] }, { "name": "optimization", "children": [ { "name": "AspectRatioBanker", "area": 7074 } ] } ] } ] } const tree = d3.hierarchy(flare) // 这里通过节点所绑定的数据中是否具有 area 属性来判断节点是否为子节点 // 如果是子节点就让求值函数返回 1(表示该节点是一个子节点) // 否则求值函数就返回 0(表示该节点是分支的中间节点) tree.sum(function (d) { return d.area ? 1 : 0; }); console.log(tree);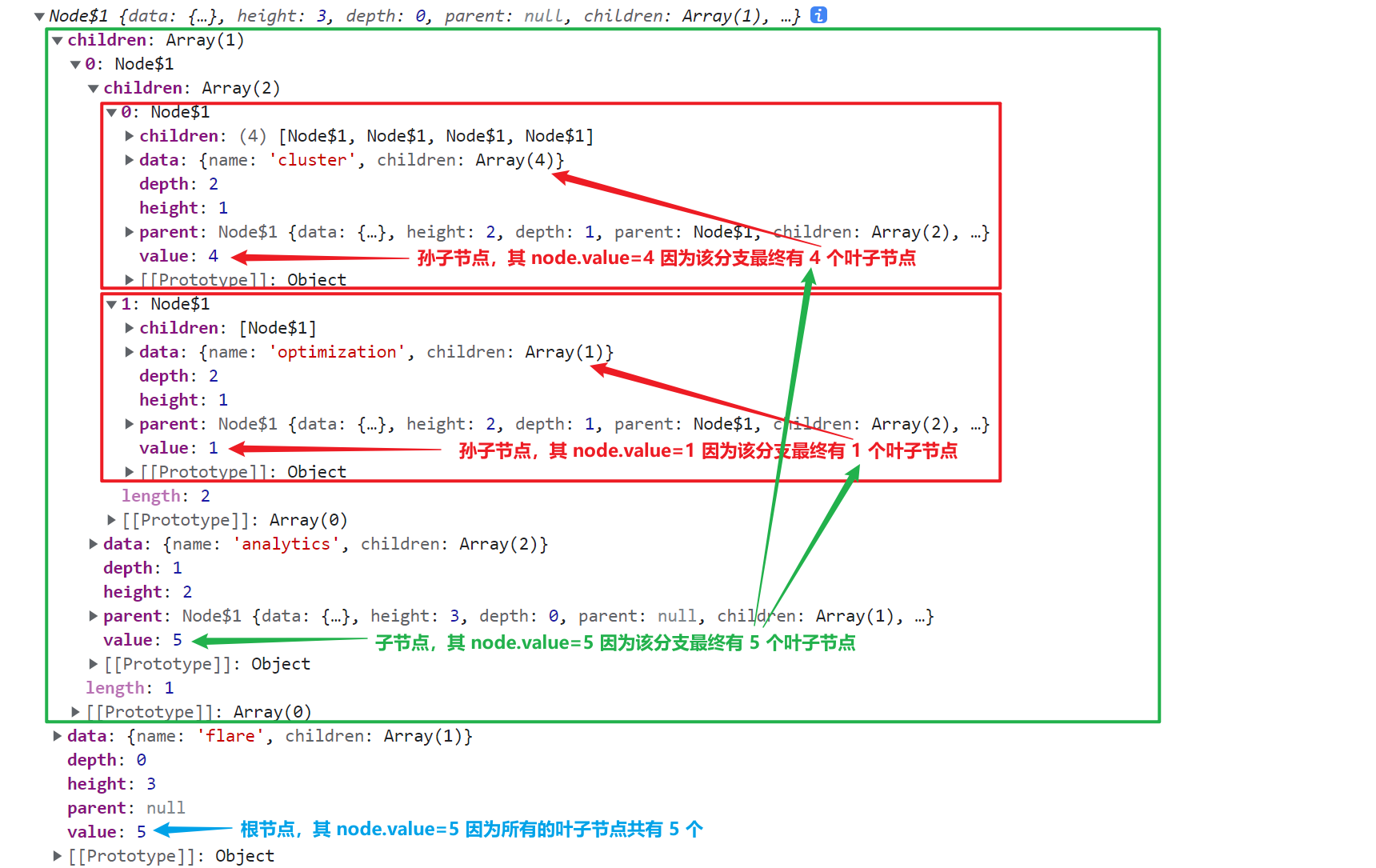
最终各节点都添加了 node.value 属性,表示该分支上的叶子节点数量 除了「魔改」
node.sum()方法,让node.value属性只表示叶子节点的和,其实还可以直接使用方法node.count(),上述场景正是该方法的所要解决的node.count()计算该节点所在的分支最后尾部有多少个叶子节点,并(从该节点开始,包含该节点)为该分支上的各节点添加一个属性node.value表示其尾部有多少个叶子节点。该方法最后返回的还是该节点对象,便于链式调用。
如果当前节点正好就是叶子节点,则只在该节点上添加node.value属性,且属性值为1
注意
在使用 d3.hierarchy(data) 计算层级结构所得到的节点上是没有 node.value 属性的。
但是在一些可视化方法中都需要使用该属性,如 d3.treemap 包裹图,需要基于该属性 node.value(累计值)来计算该节点(及其子孙节点)的面积占比大小。
所以在使用这些可视化方法时,要先调用节点的方法 node.sum(value) 或 node.count() 以在节点上添加该属性
node.sort(compare)对该节点的子节点,以及子节点的后代节点,并依次类推(从该节点开始,对该分支的同级节点),进行排序操作
参数compare是对比函数,它接受两个同级别的节点a,b作为入参compare(a, b),并返回一个数值number,根据它的正负值来决定这两个节点的排列顺序:- 如果返回的数值是负数
number < 0,表示节点a应该排在节点b前面 - 如果返回的数值是正数
number > 0,表示节点b应该排在节点a前面 - 如果返回的数值是零
number=0,则两个节点的顺序并不做限定
注意
对比函数
compare的入参是两个节点 node,这和方法node.sum(value)中value求值函数不同。求值函数
value(d)入参的是节点所绑定的数据,而compare(node_a, node_b)是节点本身。所以对比函数可以访问到节点的高度
node.height(即该节点与所在分支后最深处的叶子节点的距离)等层级结构的属性,并基于这些属性进行排序。提示
对比函数的返回值的正负值与相应的排序规则和 JS 的数组原生方法
array.sort()类似如果不想记住上面这些很繁琐的逻辑,可以使用 D3 的 d3-array 模块所提供的两个方法
d3.ascending(升序排列,值从小到大)或d3.descending(降序排列,值从大到小),使用它们作为对比函数,更具有语义化
一些可视化布局方法需要先对数据(节点)进行排序,这样可以让布局更佳,画面更有规律性:- 对于 circle-packing diagram 圆堆图推荐对同级节点的累计值进行降序 descending 排序js
root .sum(function(d) { return d.value; }) .sort(function(a, b) { return b.value - a.value; }); // 也可以使用 d3.descending 作为对比函数 // root // .sum(function(d) { return d.value; }) // .sort((a, b) => d3.descending(a.value, b.value)); - 对于 treemap 树图 和 icicle diagram 冰柱图推荐对同级节点先按照节点的高度进行降序 descending 排列,再按照节点的累计值进行降序 descending 排列js
root .sum(function(d) { return d.value; }) .sort(function(a, b) { return b.height - a.height || b.value - a.value; }); // 也可以使用 d3.descending 作为对比函数 // root // .sum(function(d) { return d.value; }) // .sort((a, b) => d3.descending(a.height, b.height) || d3.descending(a.value, b.value)); - 对于 tidy tree 紧凑的树状图 和 dendrogram 树状图推荐对同级节点先按照节点的高度进行降序 descending 排列,再按照节点的名称(字母或拼音)进行升序 ascending 排列
js// 假设节点的名称是在属性 node.id root .sum(function(d) { return d.value; }) .sort(function(a, b) { return b.height - a.height || a.id.localeCompare(b.id); });提示
任何节点都可以调用
node.sort()方法对分支后的同级节点进行排序,所以可以很方便地对不同的小分支采用不同的排序方式。只需要先对上一级节点(或根节点)先进行排序
root.sort(),然后找到特定的节点再对分支进行排序branch.sort()即可进行覆盖。- 如果返回的数值是负数
node.each(func, [that])以广度优先的顺序让当前节点(包含)所在的分支后的所有节点均调用一次函数func广度优先
广度优先 breadth-first order 是搜索树和图的基本策略之一。
广度优先搜索方法简称为 BFS,它关心的是眼下自己(入口,当前节点)能够直接到达的所有子节点,其动作有点类似于「扫描」,经过一层层的节点扫描(即同级的节点),找到可以通往下一层级的入口,最后达到最深处的叶子节点(出口)。
所以当前节点
node先调用函数func,然后是下一层的子节点依次调用函数,接着是孙子节点,依此类推,直到最深的那一层叶子节点。
第一个参数func是需要调用的函数。并向它传递三个参数func(currentNode, index, node)分别是currentNode当前所遍历的节点,index当前所遍历的节点的索引值(如果是第一个节点,也就是node,其索引值为0,并依次递增),node就是调用方法node.each()的节点(即该分支的首个节点)
(可选)第二个参数that用于改变/替代函数func里的this的指向注意
如果
node.each()设置了第二个可选参数,那么函数func就不能使用箭头函数,因为箭头函数没有自己的this,无法进行修改。
深度优先
另一个常见的搜索树和图的基本策略就是深度优先 Deep First Search,简称 DFS。
它贯彻了「不撞南墙不回头」的原则,只要没有碰壁就决不选择其它的道路,坚持向当前道路的深处挖掘(一直走到尾部的的叶子节点),常用于暴力搜索所有状态。
深度优先搜索的核心思想是试图穷举所有的完整路径,以找到可行的路径。
深度优先分作前序遍历、中序遍历、后续遍历,分别表示在遍历二叉树时,「根节点」(分支的起始节点)在被遍历时的顺序位置是最先、次之、最后。
以下的 2 个方法就是对应于深度优先分作前序遍历、后续遍历,对应于父节点和子节点以不同的先后顺序去调用函数 func。
node.eachAfter(func, [that])以后序遍历的顺序让当前节点(包含)所在的分支后的所有节点均调用一次函数func。后序遍历
采用后序遍历 post-order traversal 的方式,所以父节点需要在其子节点都调用函数后,才去调用
func函数
第一个参数func和(可选)第二个参数that的含义和上面的方法node.each()一样node.eachBefore(func, [that])以前序遍历的顺序让当前节点(包含)所在的分支后的所有节点均调用一次函数func。前序遍历
采用后序遍历 pre-order traversal 的方式,所以子节点需要在其父节点调用函数后,才去调用
func函数
第一个参数func和(可选)第二个参数that的含义和上面的方法node.each()一样
表格数据分层转换
在(使用 d3.tree() 等方法计算布局)可视化之前,需要先使用 d3.hierarchy(data) 对数据进行层级结构计算,而入参 data 一般是一个带有根节点的树形结构对象。
因为在数据分析中 CSV 文件(一般表格的一些字段之间会存在关联性,所以是有可能形成层级关系的)是十分常见的,但是对于这种扁平的数据无法直接使用 d3.hierarchy(data)进行层级结构计算(虽然可以通过定制一个复杂的子节点数据的访问函数 accessor function d3.hierarchy(data, children) 但是会让代码显得很复杂)
D3 就专门提供了一个方法 d3.stratify() 对表格形的数据进行 stratify 分层化处理。
说明
可以将 d3.stratify() 可以看作是针对表格的定制版 d3.hierarchy(),最后也是返回一个根节点对象,可以直接用于 d3.tree() 等方法计算布局。
例如对于以下表格,其中 children 字段都是唯一值,可以作为每一个数据点的唯一标识符;而字段 Parent 则表示数据点之间的(层级)关联关系
| children | parent |
|---|---|
| a | |
| b | a |
| c | a |
| d | a |
| e | b |
| f | c |
| g | c |
| h | d |
| i | h |
以上表格所表示的层级关系如下图
首先使用方法 d3.csvParse() 读取 csv 文件的数据
const table = d3.csvParse(csvContent);
// 得到以下的一个数组
// 其中每个元素都对应于 csv 表格中的一列
// [
// {child: "a", parent: ""}
// {child: "b", parent: "a"}
// {child: "c", parent: "a"}
// {child: "d", parent: "a"}
// {child: "e", parent: "b"}
// {child: "f", parent: "c"}
// {child: "g", parent: "c"}
// {child: "h", parent: "d"}
// {child: "i", parent: "h"}
// ]
// 此外该数组对象还具有一个属性 `columns`
// 它的属性值是一个数组 `["child", "parent"]`,依次列出相应的表头字段
然后使用方法 d3.stratify() 对数据进行转换
// 分层器
const stratify= d3.stratify()
.id(function(d) { return d.child; })
.parentId(function(d) { return d.parent; })
// 表格数据分层转换
// 可以得到一个根节点对象
const root = stratify(table);
以上示例的 root 结构如下
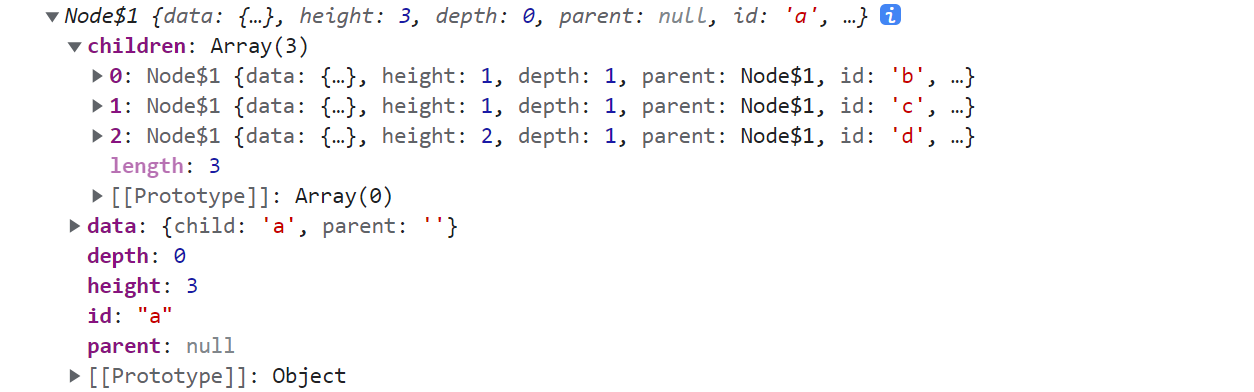
提示
d3.stratify() 和 d3.hierarchy() 返回的对象结构类似,因为这两种对象都是 node 节点对象,可以使用 result instanceof d3.hierarchy 来判断
:satisfied: 就是这么神奇!d3.hierarchy 函数对象的原型就是 Node 节点类的原型,所以可以通过 result instanceof d3.hierarchy 来判断结果是否为 node 节点对象
因此还可以在 d3.hierarchy 的原型上进行拓展,为节点 node 添加更多的功能
d3.stratify() 构建一个(参数默认的)分层器 stratify operator,以下称为 stratify。
它既是一个函数,可以直接调用 stratify(data) 传入表格数据,然后得到一个树形结构的数据(根节点对象)
它还是一个对象,具有多种方法,用以设定分层器的一些参数
stratify.id([idAccessor])用于设置数据点的唯一标识符id。
参数idAccessor是数据点唯一标识符的访问函数 accessor function,每一个数据点(即 CSV 表格中的每一行数据)都会调用该函数。该函数有两个参数idAccessor(d, i)分别是当前所遍历的数据点 datumd,以及该数据点在数据集中的索引 indexi。最后返回的是一个字符串,作为当前数据点的唯一标识符。
如果调用该方法时没有传递参数,则返回分层器的预设的访问函数,默认值如下js// 默认以数据点本身的数据作为其唯一标识符 function id(d) { return d.id; }说明
数据点的
id是用于数据层级关系 mapping 映射的,它必须是唯一标识符(不能与其他数据点的值重复)。如果该数据点是其他数据点的父节点时,则在其他数据点的属性
parentId中就会设置为该数据点的唯一标识符。因为叶子节点 leaf nodes 并不会作为其他数据点的父节点,所以它们的
id属性并不重要,可以不进行设置,则默认为undefined(如果设置为null或为空也是等价于undefined);如果设置就需要采用唯一标识符(不可与其他数据点的值重复)。stratify.parentId([parentId])用于设置数据点的父节点,通过唯一标识符来指定。
参数parentId是一个访问函数 accessor function,每一个数据点都会调用该函数。该函数有两个参数parentId(d, i)分别是当前所遍历的数据点 datumd,以及该数据点在数据集中的索引 indexi。最后返回的是一个字符串,表示当前数据点的父节点(唯一标识符)。
如果调用该方法时没有传递参数,则返回分层器的预设访问函数,默认值如下jsfunction parentId(d) { return d.parentId; }说明
根节点 root node 并没有父节点,所以它的
parentId属性值应该是undefined(也可以是null或空值)
Tree
tree 布局基于 Reingold–Tilford "tidy" algorithm 用来生成节点-链接树
d3.tree()使用默认的设置创建一个树布局生成器,以下简称为treetree(root)对指定的 root hierarchy 进行布局,并为 root 以及它的每一个后代附加两个属性:node.x- 节点的x坐标node.y- 节点的y坐标
节点的x和y坐标可以是任意的坐标系统,如你可以将x视为角度而将y视为半径,就可以生成一个 radial layout 径向布局。
可以在布局之前使用root.sort进行排序操作。